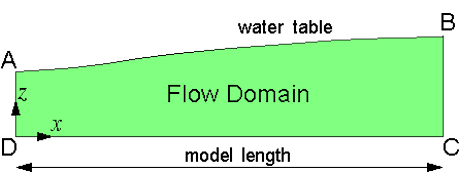
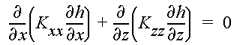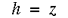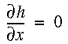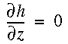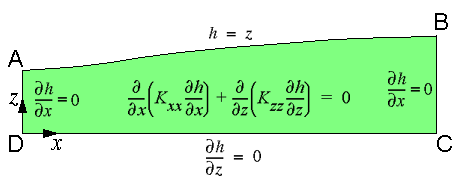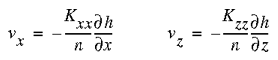Home About
TopoDrive ParticleFlow
TopoDrive ParticleFlow

Theory: TopoDrive

A topography-driven flow system is one in which ground water flows from higher-elevation recharge areas, where hydraulic head is higher, to lower-elevation discharge areas, where hydraulic head is lower.
In this setting, the main factors controlling groundwater flow are basin geometry, shape of the water table, and the distribution of hydraulic properties.

For a two-dimensional vertical section, the boundaries of the flow domain are as follows:

  • The top boundary (AB) is the water table, which is assumed to lie close to land surface.

  • The two vertical boundaries (BC and AD) and the bottom boundary (DC) are no-flow boundaries.

The no-flow boundaries might represent groundwater flow divides or low hydraulic conductivity bedrock that bounds the basin.

Note that by specifying the position of the water table, it is assumed that the pattern of recharge and discharge is such that the water table is maintained at a steady state.

TopoDrive flow domain

Steady-state flow of ground water in the vertical section is governed by the equation

TopoDrive governing equation

where h is hydraulic head, and Kxx and Kzz are the principal values of the hydraulic conductivity tensor. The principal directions are assumed to be parallel to the cartesian axes x and z.

Assuming the position of the water table is known, the boundary condition along the water table (AB) is

TopoDrive boundary condition at water table

where z is the elevation of the water table.

Along the vertical boundaries BC and AD, the no-flow boundary condition is

TopoDrive boundary condition along vertical side

Along bottom boundary CD, the no-flow boundary condition is

TopoDrive boundary condition horizontal bottom
TopoDrive mathematical problem

TopoDrive solves the above equations by the finite-element method.

The flow domain is represented by a deformed rectangular mesh, and each quadrilateral cell is divided into two triangular elements.

Linear basis functions are used to formulate the finite-element formulation.

TopoDrive finite-element mesh

After solving for hydraulic head h, the x and z components of the groundwater velocity vector are computed by

TopoDrive groundwater velocity computation

where n is porosity. The velocity vectors are used for calculating flow paths and the advective movement of fluid particles.